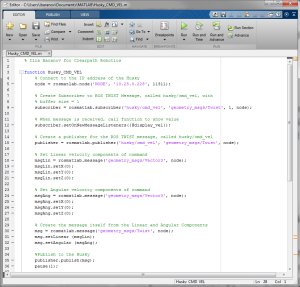
Clearpath Robotics recently tested the capabilities of the ROS for MATLAB toolkit (available here: robot-operating-system.html). This is very interesting for the research and education fields, as it will allow users to take their existing MATLAB code and use it on a real world robot with little modification.
Here, we do a quick test by driving the Husky remotely using MATLAB. This showcases a small portion of the abilities that MATLAB presents us. If you already have a Husky (or a virtual one), and have MATLAB 2013a or 2013b installed, you can try this out right now!
- Install the toolkit from the link above
- Download our sample code: Husky_CMD_VEL.m
- Replace the IP address with the address of your Husky.
- Alternatively, use a virtual Husky as described here: Drive a Husky
- Try it out!
Below, we can see the output of one such run session.


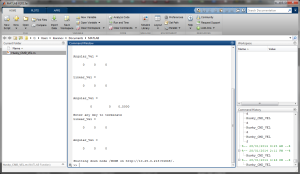
For a differentially-steered robot, issuing constant forward velocity, ‘v’, and turn rate, ‘w’ commands will result in the robot following a circular path with radius= v/w. Is this also valid for the Husky, which is a skid steer robot? From my sample program, it does not appear to be so, since the Husky drifts fairly quickly from a circular path. OR, am I seeing effects caused by the realistic modeling of friction between the tires and floor?
You are correct that the difference you are seeing comes from the friction between the tires and the floor. The underlying motion model between the two types of robots is the same, however, since a skid-steer robot has two tires on each side that are rotating at the same rate, there will be slippage occurring on both sides of the vehicle which will create friction that reduces the turning rate (or increases the turning radius). This isn’t the case with two-wheeled robots which have very little slippage when turning. There are different ways to model this motion, many of these methods put factors on the turning radius that are dependent on the relative velocities between the left and right tires. See for example: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4481911/ This slippage is also dependant on the ground surface. I am not familiar with the motion model that gazebo uses for the husky if you are describing your simulated results.